Thermo-Hydraulische Simulation: Ein Deepdive

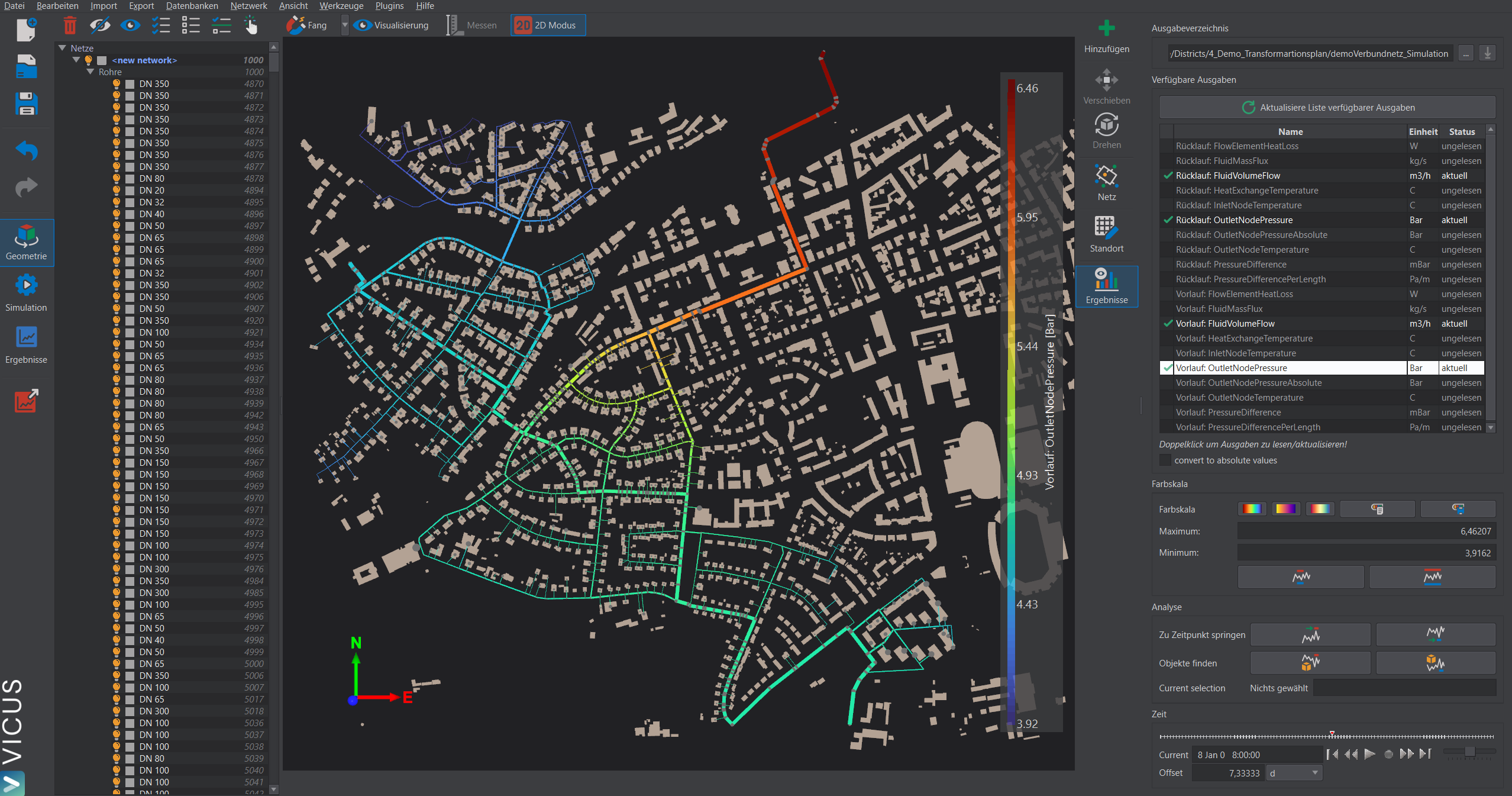
Die Energiewende verändert nicht nur die Wärmeversorgung, sondern auch die Art und Weise, wie wir Wärmenetze planen und betreiben. Moderne, dynamische Netze – von Kalter Nahwärme bis hin zu Fernwärmesystemen mit dezentralen Erzeugern – erfordern neue mathematische Werkzeuge. Dieser Beitrag zeigt, welche Physik und Numerik in VICUS Districts steckt.

Die Zeit der starren Fernwärmesysteme mit einem zentralen Erzeuger, klarer Fließrichtung und konstanten Temperaturen ist vorbei. Ob kalte Anergienetze oder Fernwärmenetze mit mehreren, dynamisch zuschaltbaren Einspeisern: Die Komplexität steigt erheblich.

Für Planer*innen bedeutet das: Simulation ist nicht mehr „nice to have“, sondern ein operatives Werkzeug, um Netze sicher, effizient und realitätsnah auszulegen.

Das Kernproblem: Temperatur und Strömung beeinflussen sich gegenseitig

Früher wurden Hydraulik (Druck, Massenstrom) und Thermik (Temperatur) oft getrennt berechnet. Für klassische Hochtemperaturnetze funktionierte das leidlich. In modernen Niedertemperaturnetzen und in Fernwärmenetzen mit dezentralen Einspeisern greift diese Vereinfachung jedoch zu kurz.

Denn: Die Temperatur beeinflusst zentrale Stoffgrößen wie Dichte oder Viskosität des Fluids – und damit Strömung, Druckverluste und Wärmetransport. Aber nicht nur das: dynamische Regelungen ändern z.B. Ventilstellungen aufrgund der Temperatur.
Der Mechanismus lässt sich vereinfacht so beschreiben:

1. Temperatur ändert Regelungsgrößen und Fluidparameter
2. Diese bestimmen den hydraulischen Widerstand
3. Der Widerstand bestimmt den Massenstrom
4. Der Massenstrom transportiert Wärme – und beeinflusst wiederum die Temperatur

Für realistische Simulationen müssen daher Thermik und Hydraulik gekoppelt berechnet werden.

Die Mathematik von thermo-hydraulischer Simulation

Moderne Simulationssolver wie der in VICUS Districts integrierte wissenschaftliche NANDRAD-Solver beschreiben Wärmenetze als Graph aus Knoten und Kanten (Rohre, Ventile, Pumpen, Erzeuger, Verbraucher). Hydraulische und thermische Modelle sind klar getrennt formuliert, werden aber iterativ miteinander verknüpft.

1. Das hydraulische Modell (stationär)

Druckwellen breiten sich in nahezu inkompressiblen Fluiden sehr schnell aus. Deshalb wird die Hydraulik als stationäres, algebraisches Gleichungssystem gelöst.

Massenerhaltung an jedem Knoten:

Für jeden Knoten i gilt, dass die Summe aller ein- und austretenden Massenströme Null ergeben muss (1. Kirchhoffsches Gesetz):

$$\sum_k \dot{m}_{i,k} = 0$$Impulserhaltung / Druckverlust im Rohr:

Zwischen dem Einlassdruck $p_{in}$ und Auslassdruck $p_{out}$ eines Elements (z.B. Rohr) besteht eine Druckdifferenz, die vom Massenstrom und der Temperatur abhängt. Die allgemeine Funktion lautet:

$$p_{\text{in},j} – p_{\text{out},j} = \frac{l}{2 d_i} \, \lambda(Re) \, \rho \, |v_j| v_j$$

Hierbei ist $v_j$ die Fließgeschwindigkeit.

Der Reibungsbeiwert hängt über die Reynolds-Zahl vom Strömungszustand ab:

$$Re = \frac{v \, d_i}{\nu(T)}$$

Die Abhängigkeit von $\nu(T)$ wird hier berücksichtigt.

Der Durckverlust von Rohrleitungen wird dabei über die Gleichung nach Colebrook-White berechnet.

$\dot{m}$	Massenstrom
$p$	Druck
$l$, $d$	Rohrlänge und Durchmesser
$v$	Geschwindigkeit
$Re$	Reynoldszahl
$\lambda$	Rohrreibungskoeffizient
$h$	Enthalpie
$\dot{Q}$	Wärmestrom
$T$	Temperatur
$C$	Wärmekapazität

2. Das thermische Modell (dynamisch)

Temperaturen ändern sich vergleichsweise langsam – deshalb wird das thermische Verhalten zeitabhängig berechnet.

Energiebilanz eines Rohrvolumens:

$$C_k \frac{\partial T_k}{\partial t} = \dot{H}_{\text{in},k} – \dot{H}_{\text{out},k} – \dot{Q}_{\text{loss},k}$$

Wärmeverluste ans Erdreich oder Gebäudeumfeld:

$$\dot{Q}_{\text{loss},k} = (T_k – T_{\text{amb}}) \cdot UA_{\text{pipe}}$$

Wie sich die Gleichungen numerisch lösen lassen

Für die Kopplung von Thermik und Hydraulik wenden wir eine zweistufige Strategie an:

1. Hydraulisches Modell:
   Die Glechungen sind stationär und somit nicht zeitabhängig. Es ergibt sich ein nichtlineares algebraisches Gleichungssystem. Dieses wird mit dem Newton-Raphson gelöst.
2. Thermisches Modell:
   Die thermischen Gleichungen sind aufgrund der Kapazität des Fluides zeitabhängig. Es ergeben sich somit Differentialgleichungen. Diese werden mit einem effizienten numerischen Verfahren (CVODE) gelöst. Die ist ein implizites Mehrschrittverfahren, auch backward differentiation formula (BDF) genannt.

Das Ergebnis ist ein extrem performantes Verfahren, das selbst große Netze mit vielen dezentralen Erzeugern und Prosumer-Strukturen zuverlässig berechnet.

Software für die Wärmenetzsimulation

Die Landschaft der Simulationswerkzeuge teilt sich in domänenspezifische Codes und allgemeine Modellierungssprachen.

Modelica: Der Standard für Forschung

Modelica hat sich als Standard für die Forschung etabliert. Durch die akausale Modellierung („Gleichungen statt Algorithmen“) eignet es sich hervorragend für komplexe, bidirektionale Komponenten. Bibliotheken wie die Buildings Library oder AixLib bieten vorgefertigte Modelle für Rohre und Prosumer.

VICUS Districts: Intuitive Anwendung für die Praxis

Unsere spezialisierte Software für die Simulation von Quartieren und Wärmenetzen ist VICUS Districts.

• Architektur: Die Software basiert auf C++ und nutzt den integrierten numerischen Solver. Dies sorgt für eine hohe Rechenperformance auch bei großen Netzen mit Hunderten von Teilnehmern.
• Methodik: VICUS implementiert genau den oben beschriebenen Ansatz: Eine strikte Trennung von hydraulischen (algebraischen) und thermischen (differentiellen) Gleichungssystemen, die jedoch eng gekoppelt gelöst werden.
• Besonderheit: Durch die intuitive Nutzeroberfläche kann ein echtes thermo-hydraulisches Simulationsmodell in sehr kurzer Zeit erstellt werden. Neben dem effizienten numerischen Solver ist ein besonders detailliertes Erdreichmodell implementiert, welches gekoppelt mit dem Netz simuliert wird.

Darüberhinaus existieren weitere meist webbasierte Tools zur vereinfachten Berechnung von Wärmenetzen, wie z.B. nPro. Diese eignen sich meist für frühe Planungspahsen. Eine „echte“ thermo-hydraulische Berechnung bieten diese jedoch nicht.

Warum das für Ihr Projekt wichtig ist

Die beschriebene Kopplung ist nicht theoretischer Luxus, sondern die Grundlage für realistische Simulationen modernster Wärmenetze:

Dezentrale Erzeuger in Fernwärmenetzen

Biomasse, BHKW, Großwärmepumpen, Solarthermie, industrielle Abwärme – moderne Fernwärmenetze haben viele potenzielle Einspeiser.
Mit VICUS Districts lässt sich simulieren:

• Wie ändern sich Fließrichtungen bei wechselnder Einspeisung?
• Wie interagieren Erzeuger hydraulisch und thermisch?
• Welche Strategien minimieren Pumpstrom und Rücklauftemperaturen?

Kalte Nahwärme (Anergienetze)

Hier spielt zusätzlich die Interaktion mit dem Erdreich eine wichtige Rolle:

• Langzeitverhalten des Bodens (Auskühlung, Vereisungsrisiko)
• Wärmepumpen-Effizienz bei variablen Strömungen
• Bidirektionale Strukturen durch Prosumer

Nur eine thermo-hydraulisch gekoppelte Simulation erlaubt die Bestimmung des optimalen Betriebs („Sweet Spot“ zwischen Pumpstrom und Wärmepumpeneffizienz).

Fazit

Moderne Wärmenetze – egal ob Kalte Nahwärme oder Fernwärmesysteme mit mehreren dezentralen Erzeugern – lassen sich nicht mehr mit vereinfachten Excel-Ansätzen planen. Sie erfordern eine realitätsnahe Modellierung der physikalischen Kopplung von Druck, Massenstrom und Temperatur.

Mit VICUS Districts bringen wir die wissenschaftliche Tiefe unseres Simulationssolvers in eine anwenderfreundliche Oberfläche. Damit können Sie Netze entwickeln, die nicht nur theoretisch funktionieren, sondern auch im Betrieb zuverlässig, effizient und zukunftssicher sind.